On a straight road going through a village there are two log cabins, 50 meters apart. Where on the road should we build a park so that the total distance from the cabins to the park would be as small as possible?
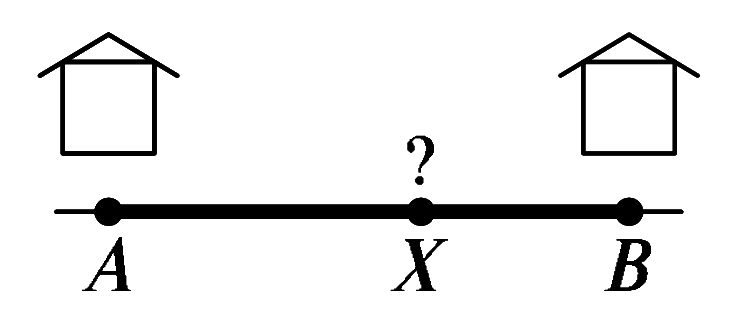
If we were doing this fairly, the park would be halfway between the two cabins, 25 meters from each cabin, adding up to 50 meters. However, in our problem, the park X can be anywhere on the road between cabins A and B because added together, segments AX and XB will always add up to 50 meters. (For example, if we put the park 10 meters from cabin A, then cabin B would be 40 meters away from it, adding up to 50 meters.)
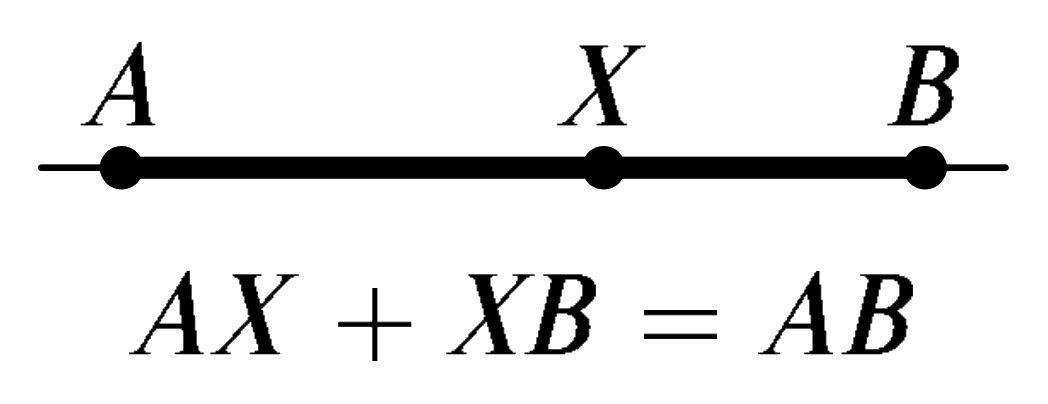
Now solve the same problem with three and four cabins instead of two. Each cabin is 50 meters apart from the next; where, now, should we put the park?
The case of three cabins: if we do not take into account the middle cabin, then any point between the first and last cabin would satisfy our conditions. Therefore, the best position for the park is next to the middle cabin.
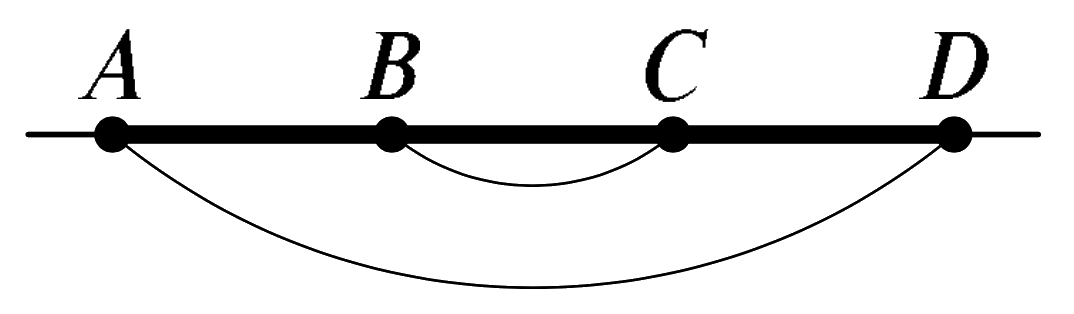
With four cabins (we will call them A, B, C, and D), let us consider the cabins on the sides (A and D) separately from the middle cabins (B and C). For cabins A and D, any point on line segment AD will work. The distances to A and D from the park will always add up to 150 meters.
Similarly, for cabins B and C, any point on line segment BC will work. The sum of the distances to B and C from the park will always be 50 meters. Thus the minimum total distance (200 meters) is achieved by building the park anywhere between cabins B and C.
CAN YOU HELP US NOW?
100 students live in village A, and 50 in village B. The villages are 3 kilometers apart. If Competitive Kids STEM (CKSTEM) is trying to minimize the total distance of the students' walks to school, where should CKSTEM build the school?
Most likely your intuition will not give you a correct answer. You need to bring math in action to help us find a good place to build a school so that total distance walked by the students is minimum. We understand schools are closed during COVID-ERA but we have to plan for the future. Can you help us out by providing your comments below?
Numbers are less important to us. We believe in proofs. Can you provide a good proof to support your answer to make it easy for us to accept your recommendation?
Yashnoor It should be 1 km from the school A and 2 from B. This would mean that each group of children will walk the same length. (100*1=100 for group A and 50*2=100 for B)
January 15, 2021, 11:09pm ·Yogesh @Yashnoor@yashnoor how do you know that it is the minimum distance? If school is 0.5 km away A then the total distance will be 50+125 = 175 km which is less than what you have calculated. Can we keep make it even smaller? Try to put together a proof.
January 16, 2021, 02:24am ·- January 16, 2021, 05:32pm ·
- January 16, 2021, 05:35pm ·
- January 18, 2021, 01:58am ·
Anoushka Guliani i would put it near school a (with 100 students) because as there is twice the amount of kids there as school b (50 students) they wouldn't have to walk as far, but school b (50 students) would have to walk 3 km to reach the park.
February 17, 2022, 12:54am ·
Yashnoor It should be 1 km from the school A and 2 from B. This would mean that each group of children will walk the same length. (100*1=100 for group A and 50*2=100 for B)
Yogesh @Yashnoor@yashnoor how do you know that it is the minimum distance? If school is 0.5 km away A then the total distance will be 50+125 = 175 km which is less than what you have calculated. Can we keep make it even smaller? Try to put together a proof.
Anoushka Guliani i would put it near school a (with 100 students) because as there is twice the amount of kids there as school b (50 students) they wouldn't have to walk as far, but school b (50 students) would have to walk 3 km to reach the park.